Function composition is a way of combining two functions to produce a new function. If we have a function $f :: b \to c$ and a function $g :: a \to b$, we can combine $f$ and $g$ to produce a new function $f \circ g :: a \to c$. In Haskell this is defined as f . g = \x -> f (g x). So “f compose g” means call g with an argument, and pass the result as the argument to f. We can use this to assemble chains of multiple functions such as a . b . c . ….

Composed functions are read right-to-left; f = a . b . c is equivalent to f x = a (b (c x)). So if we have a composed function (++ "!") . (++ " world") . reverse and call it with “olleh”, it will first be reversed to give “hello”, then have “world” appended, then “!” to give us “hello world!”.

I recently had a case where I wanted to compose functions, but I was thinking about the problem in a slightly different way. Rather than composing right-to-left, I wanted to perform a series of operations, and chain the output from the first function into the input of the second function, and so on.

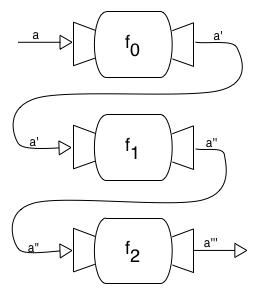
In other words, I wanted left-to-right composition, rather than right-to-left. To do this we can define a new operator to reverse the order in which functions are composed.

(>>>) :: (a -> b) -> (b -> c) -> (a -> c)
f >>> g = g . f     -- or: (>>>) = flip (.)

{-- Left-to-right vs. right-to-left composition:

ghci> reverse >>> (++" world") >>> (++"!") $ "olleh"
"hello world!"

ghci> (++"!") . (++ " world") . reverse $ "olleh"
"hello world!"

--}

It turns out that Haskell already has this operator defined in Control.Arrow, so all I really needed was import Control.Arrow.

As an aside, I also realised that Haskell lets us use line-breaks and indents if we want to write either form of composition in a more imperative style, similar to do-notation:

transforms :: String -> String
transforms =
    reverse
    >>> (++ " world")
    >>> (++ "!")